구글 코랩 사용해서 실습했습니다~!

차원과 차원축소
데이터가 가진 속성을 특성이라 부른다.
과일사진의 경우 10,000개의 픽셀이 있기 때문에 10,000개의 특성이 있는 셈이다.
이런 특성을 차원이라고 부른다.
이 차원을 줄일 수 있다면 저장공간을 크게 절약할 수 있을 것이다.
비지도 학습 중 하나인 차원축소 알고리즘
대표적인 차원축소 알고리즘인 주성분분석 = PCA
기술적인 이유로 주성분은 원본 특성의 개수와 샘플 개수 중 작은 값 만큼 찾을 수 있다.
일반적으로 비지도 학습은 대량의 데이터에서 수행하기 때문에 원본 특성의 개수만큼 찾을 수 있다고 말한다.
앞 장과 동일하게 사진을 불러온다.
!wget https://bit.ly/fruits_300_data -O fruits_300.npy
import numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1, 100*100)from sklearn.decomposition import PCA
pca = PCA(n_components=50)
pca.fit(fruits_2d)import matplotlib.pyplot as plt
def draw_fruits(arr, ratio=1):
n = len(arr) # n은 샘플 개수입니다
# 한 줄에 10개씩 이미지를 그립니다. 샘플 개수를 10으로 나누어 전체 행 개수를 계산합니다.
rows = int(np.ceil(n/10))
# 행이 1개 이면 열 개수는 샘플 개수입니다. 그렇지 않으면 10개입니다.
cols = n if rows < 2 else 10
fig, axs = plt.subplots(rows, cols,
figsize=(cols*ratio, rows*ratio), squeeze=False)
for i in range(rows):
for j in range(cols):
if i*10 + j < n: # n 개까지만 그립니다.
axs[i, j].imshow(arr[i*10 + j], cmap='gray_r')
axs[i, j].axis('off')
plt.show()draw_fruits(pca.components_.reshape(-1, 100, 100))
이 주성분은 원본데이터에서 가장 분산이 큰 방향을 순서대로 나타낸것.
주성분을 찾았으므로 원본 데이터를 주성분에 투영하여 특성의 개수를 10,000개에서 50개로 줄일 수 있다.
print(fruits_2d.shape)
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)
데이터가 성공적으로 줄여졌다. (1/200로)
fruits_2d대신 fruits_pca를 저장한다면 훨씬 공간을 줄일 수 있다!
원본 데이터 재구성
앞에서 10,000개의 특성을 50개로 줄였다.
이로 인해 어느정도 손실이 발생할 수밖에 없지만, 최대한 분산이 큰 방향으로 데이터를 투영했기 때문에 원본 데이터를 상당 부분 재구성할 수 있습니다.
fruits_inverse = pca.inverse_transform(fruits_pca)
print(fruits_inverse.shape)
10,000개의 특성이 복원되었다.
100*100크기로 바꾸어 100개씩 나누어 출력하면
fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)
for start in [0, 100, 200]:
draw_fruits(fruits_reconstruct[start:start+100])
print("\n")


거의 모든 과일이 잘 복원되었다.
일부 흐리고 번진 부분이 있지만, 성공적이라 볼 수 있다.
이는 50개의 특성이 분산을 가장 잘 보존하도록 변환된 것이기 때문이다.
설명된 분산
주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한 값 = 설명된 분산
print(np.sum(pca.explained_variance_ratio_))
92%가 넘는 분산을 유지하고 있다.
앞에서 50개의 특성에서 원본 데이터를 복원했을 때 원본 이미지의 품질이 높았던 이유를 여기에서 찾을 수 있다.
plt.plot(pca.explained_variance_ratio_)
plt.show()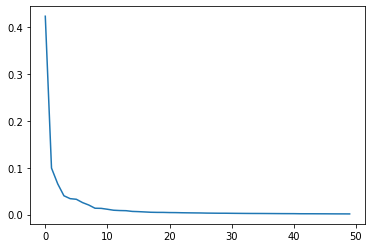
그래프를 보면 처음 10개의 주성분이 대부분의 분산을 표현하고 있다.
그 다음부터는 각 주성분이 설명하고 있는 분산은 비교적 작다.
과일사진 원본 데이터와 PCA로 축소한 데이터를 지도학습에 적용해보고 어떤 차이가 있는지 알아보자.
3개의 과일사진을 분류해야 하므로 로지스틱 회귀모델을 사용한다.
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()target = np.array([0]*100 + [1]*100 + [2]*100)from sklearn.model_selection import cross_validate
scores = cross_validate(lr, fruits_2d, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
교차검증의 점수는 0.997 정도로 매우 높다.
scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))50개의 측성만 사용했는데도 정확도가 100%이고 훈련시간은 0.02초로 엄청나게 감소했다.
pca = PCA(n_components=0.5)
pca.fit(fruits_2d)print(pca.n_components_)
단 2개의 특성만으로 원본 데이터에 있는 분산의 50%를 표현할 수 있다.
fruits_pca = pca.transform(fruits_2d)
print(fruits_pca.shape)scores = cross_validate(lr, fruits_pca, target)
print(np.mean(scores['test_score']))
print(np.mean(scores['fit_time']))
2개의 특성을 사용하고도 99%의 정확도를 달성!
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_pca)
print(np.unique(km.labels_, return_counts=True))for label in range(0,3):
draw_fruits(fruits[km.labels_ == label])
print("\n")


for label in range(0,3):
data = fruits_pca[km.labels_ == label]
plt.scatter(data[:,0], data[:,1])
plt.legend(['apple', 'banana', 'pineapple'])
plt.show()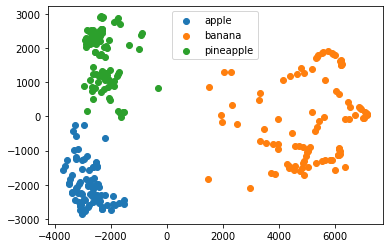
데이터를 시각화하면 예상치 못한 통찰을 얻을 수 있다.
그런면에서 차원 축소는 매우 유용한 도구이다.
출처: http://www.yes24.com/Product/Goods/96024871
혼자 공부하는 머신러닝+딥러닝 - YES24
- 혼자 해도 충분하다! 1:1 과외하듯 배우는 인공지능 자습서 이 책은 수식과 이론으로 중무장한 머신러닝, 딥러닝 책에 지친 ‘독학하는 입문자’가 ‘꼭 필요한 내용을 제대로’ 학습할 수 있
www.yes24.com
'Machine Learning > 혼자 공부하는 머신러닝+딥러닝' 카테고리의 다른 글
| 7-2 심층신경망 (0) | 2022.01.23 |
|---|---|
| 7-1 인공신경망(혼자공부하는 머신러닝 딥러닝) (0) | 2022.01.04 |
| 6-2.p303~ k-평균 (0) | 2021.10.29 |
| 6-1.p286~ 군집 알고리즘 (0) | 2021.10.28 |
| 5-3.p263~ 트리의 앙상블 (0) | 2021.10.28 |